Geometría descriptiva

La geometría descriptiva es la rama de la geometría por la cual se representan los objetos en tres dimensiones en una superficie plana o en dos dimensiones.
También se puede definir como la disciplina que se encarga del estudio de las propiedades geométricas y de la relación espacial de las figuras partiendo de sus proyecciones ortogonales sobre una superficie plana. Es muy importante porque se utiliza en numerosas disciplinas como la ingeniería, la arquitectura, el diseño de interiores entre otras.

¿Qué es la geometría descriptiva?

La geometría descriptiva es una rama de la geometría que se centra en la representación de objetos tridimensionales y sus relaciones espaciales a través de dibujos bidimensionales. Proporciona un enfoque sistemático para describir y visualizar con precisión estructuras tridimensionales complejas sobre una superficie plana, normalmente utilizando técnicas de proyección ortográfica.

Objeto de la geometría descriptiva

El objetivo principal de la geometría descriptiva es comunicar y transmitir información espacial, particularmente en los campos de la ingeniería, la arquitectura y el diseño. Permite a diseñadores, ingenieros y dibujantes crear dibujos técnicos precisos que representan con precisión el tamaño, la forma y la disposición de los objetos en un espacio tridimensional.

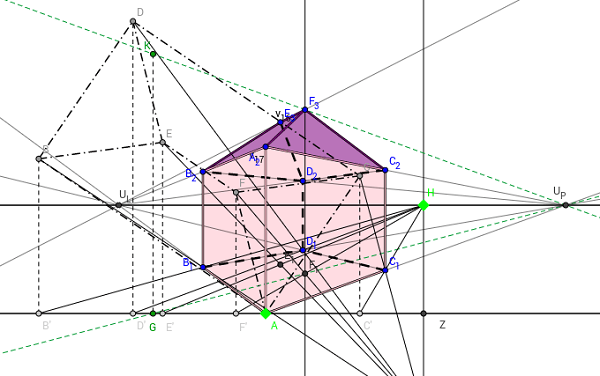
La geometría descriptiva establece los principios, para resolver y comunicar gráficamente los diferentes elementos en el espacio. Estos elementos son: puntos, rectas, superficies planas o curvas, sólidos o volúmenes en doble proyección ortogonal.
La geometría descriptiva emplea un conjunto de principios, reglas y técnicas establecidas para representar objetos tridimensionales en dos dimensiones. Estas técnicas incluyen:

1. Proyección ortográfica: La proyección ortográfica es la técnica principal utilizada en geometría descriptiva. Implica proyectar el objeto tridimensional en dos o más planos mutuamente perpendiculares (normalmente los planos superior, frontal y lateral). Al registrar las proyecciones del objeto en estos planos, se logra una representación completa y precisa de las características y dimensiones del objeto.

2. Vistas auxiliares: Las vistas auxiliares son vistas ortográficas adicionales que se utilizan para representar la verdadera forma y tamaño de un objeto cuando no es paralelo a ninguno de los planos ortográficos primarios. Estas vistas proporcionan una representación más detallada y precisa de objetos complejos mostrándolos desde diferentes perspectivas.

3. Vistas en sección: las vistas en sección se utilizan para revelar la estructura interna o los detalles de un objeto. Al cortar o “seccionar” el objeto a lo largo de un plano particular y luego representar la superficie cortada en una proyección ortográfica, las vistas en sección proporcionan una comprensión clara de las características internas y las relaciones del objeto.

4. Intersección y desarrollo: la geometría descriptiva también se ocupa de determinar las intersecciones entre elementos geométricos y desarrollar patrones planos o representaciones desplegadas de superficies curvas. Estas técnicas son particularmente útiles en campos como la fabricación de chapa metálica, donde se requieren patrones planos precisos para cortar y dar forma a materiales.

En general, la geometría descriptiva proporciona un método preciso y estandarizado para representar objetos tridimensionales en dibujos bidimensionales. Ser trata de una herramienta vital en las disciplinas de ingeniería, arquitectura y diseño, permitiendo una comunicación, visualización y análisis efectivos de relaciones espaciales complejas.

La que hoy conocemos como geometría descriptiva, es la elaborada por el matemático francés Gaspar Monge, quien ideó un  método de  representación de formas y cuerpos para representarlas en un plano, sea cual fuesen sus dimensiones.
Gracias a este método, se utiliza un plano horizontal o iconográfico, en el cual se dibuja lo que se ve si se viera la imagen desde el infinito de la parte superior, y un plano vertical u ortográfico para representarlo  viéndolo desde uno de los costados.
Gracias al descrubrimiento de Monge es posible conocer la forma y posición de un cuerpo en el espacio viendo su dibujo sobre un plano, resolviendo con esto numerosos problemas de carácter analítico.

¿En qué se diferencia la geometría descriptiva de otras ramas de la geometría?

La geometría descriptiva se diferencia de otras ramas de la geometría en su enfoque específico en la representación de objetos tridimensionales y sus relaciones espaciales a través de dibujos bidimensionales. A continuación se muestran algunas formas clave en las que la geometría descriptiva se distingue de otras ramas de la geometría:

Dimensionalidad: La geometría descriptiva se ocupa principalmente de objetos tridimensionales y sus características espaciales. Implica proyectar estos objetos en planos bidimensionales para crear representaciones precisas. Por el contrario, otras ramas de la geometría, como la geometría euclidiana o la geometría proyectiva, suelen centrarse en figuras bidimensionales y sus propiedades.

Visualización y representación: la geometría descriptiva se ocupa principalmente de visualizar y representar objetos tridimensionales en un plano bidimensional. Sus técnicas, como la proyección ortográfica, las vistas en sección y las vistas auxiliares, están desarrolladas específicamente para capturar con precisión el tamaño, la forma y la disposición de los objetos en un espacio tridimensional. Este énfasis en la visualización y la representación distingue a la geometría descriptiva de otras ramas que pueden centrarse más en propiedades teóricas o conceptos abstractos.

Aplicación y propósito: La geometría descriptiva tiene aplicaciones prácticas en campos como la ingeniería, la arquitectura y el diseño. Proporciona un enfoque sistemático para crear dibujos técnicos y comunicar información espacial. Sus técnicas y principios están diseñados para satisfacer las necesidades de estas disciplinas aplicadas. Por el contrario, otras ramas de la geometría pueden tener aplicaciones teóricas o matemáticas más amplias que se extienden más allá de campos específicos.

Reglas y técnicas: la geometría descriptiva tiene su propio conjunto de reglas, principios y técnicas que son distintas de las que se encuentran en otras ramas de la geometría. Estas reglas gobiernan la proyección de objetos tridimensionales en planos bidimensionales y la representación de relaciones espaciales complejas. Las técnicas de geometría descriptiva, como la determinación de intersecciones y el desarrollo de patrones planos, son específicas de esta rama y no suelen encontrarse en otras áreas de la geometría.

Visualización de relaciones complejas: la geometría descriptiva proporciona un marco para visualizar y comprender relaciones espaciales complejas. Permite la representación de objetos desde diferentes perspectivas, la visualización de estructuras internas a través de vistas en sección y la determinación de intersecciones entre elementos geométricos. Este enfoque en representar y comprender las relaciones espaciales distingue a la geometría descriptiva de otras ramas que pueden concentrarse más en pruebas teóricas o conceptos abstractos.

En resumen, la geometría descriptiva se diferencia de otras ramas de la geometría en su enfoque en la representación de objetos tridimensionales a través de dibujos bidimensionales, sus aplicaciones prácticas en campos aplicados, sus reglas y técnicas específicas y su énfasis en visualizar relaciones espaciales complejas.

¿Cuáles son algunas técnicas comunes utilizadas en geometría descriptiva para representar con precisión objetos tridimensionales?

La geometría descriptiva emplea varias técnicas para representar con precisión objetos tridimensionales en dibujos bidimensionales. A continuación se muestran algunas técnicas comunes utilizadas en geometría descriptiva:

a) Proyección Ortográfica: La proyección ortográfica es la técnica fundamental en geometría descriptiva. Implica proyectar el objeto tridimensional en dos o más planos mutuamente perpendiculares, normalmente los planos superior, frontal y lateral. Al registrar las proyecciones del objeto en estos planos se consigue una representación completa y precisa de sus características y dimensiones. La proyección ortográfica proporciona múltiples vistas del objeto, lo que permite una comprensión integral de su forma y relaciones espaciales.

b) Vistas auxiliares: Las vistas auxiliares son vistas ortográficas adicionales que se utilizan para representar la verdadera forma y tamaño de un objeto cuando no es paralelo a ninguno de los planos ortográficos primarios. Estas vistas proporcionan una representación más detallada y precisa de objetos complejos mostrándolos desde diferentes perspectivas. Las vistas auxiliares se crean proyectando el objeto en un plano paralelo a una de sus caras o aristas. Esta técnica ayuda a visualizar las verdaderas dimensiones del objeto y ayuda a representar con precisión sus características.

c) Vistas en sección: las vistas en sección se utilizan para revelar la estructura interna o los detalles de un objeto. Al cortar o “seccionar” el objeto a lo largo de un plano particular y luego representar la superficie cortada en una proyección ortográfica, las vistas en sección proporcionan una comprensión clara de las características internas y las relaciones del objeto. Las vistas en sección son especialmente útiles cuando se representan objetos con interiores complejos o cuando se resaltan detalles específicos que no son visibles en las vistas exteriores.

d) Determinación de intersecciones: la geometría descriptiva también implica determinar intersecciones entre elementos geométricos, como líneas, planos o superficies. Estas intersecciones son cruciales para representar con precisión las relaciones entre diferentes partes de un objeto tridimensional. Se utilizan técnicas como la intersección de líneas, planos o superficies para determinar puntos, curvas o perfiles precisos donde los elementos se cruzan.

e) Desarrollo de Superficies: La geometría descriptiva incluye técnicas para desarrollar patrones planos o representaciones desplegadas de superficies curvas. Esto es particularmente útil en campos como la fabricación de chapa o la confección de patrones. Al desplegar cuidadosamente y representar la superficie en un plano bidimensional, se pueden obtener patrones planos precisos, que sirven como plantillas para cortar y dar forma a los materiales.

f) Proyección en perspectiva: si bien la proyección ortográfica es la técnica principal en geometría descriptiva, la proyección en perspectiva se emplea ocasionalmente para crear una representación más realista de objetos tridimensionales. La proyección en perspectiva utiliza puntos de fuga y líneas convergentes para representar con precisión el escorzo y la percepción de profundidad del objeto. Aunque no se usa con tanta frecuencia en dibujos técnicos, la proyección en perspectiva puede ser valiosa para representaciones arquitectónicas y artísticas.

Estas técnicas de geometría descriptiva proporcionan un enfoque sistemático y estandarizado para representar con precisión objetos tridimensionales en dibujos bidimensionales. Al emplear estas técnicas, los diseñadores, ingenieros y dibujantes pueden comunicar información espacial de manera efectiva y visualizar estructuras complejas.